영넌 개발로그
[밑시딥3] 미분 자동 계산 2 - 역전파 본문
개인 공부용 포스팅
역전파 (backpropagation, 오차역전파법) ?
미분을 효율적으로 계산할 수 있고 결괏값의 오차도 수치 미분보다 작음
연쇄 법칙 (chain rule)
여러 함수를 사슬처럼 연결하여 사용하는 모습을 빗댄 것
연쇄 법칙에 따르면 합성함수의 미분은 구성 함수 각각을 미분한 것과 같음
예시 ) y = F(x) 는 a = A(x), b = B(a), y = C(b) 라는 세 함수로 구성되어 있음
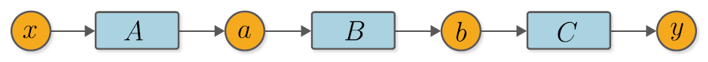
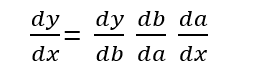
x에 대한 y의 미분은 구성 함수 각각의 미분값을 모두 곱한 값과 같음
합성 함수의 미분은 각 함수의 국소적인 미분들로 분해 가능하다 == 연쇄법칙
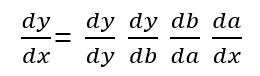
dy/dy 는 자신에 대한 미분이라서 항상 1.
생략하는 것이 보통이나 역전파를 구현할 때는 표시하는 게 이해가 편함
역전파 원리 도출
x에 대한 y의 미분 식을 출력 쪽의 미분부터 순서대로 계산하면 dy/dx가 결과로 나옴 (출력 y에서 입력 x방향)


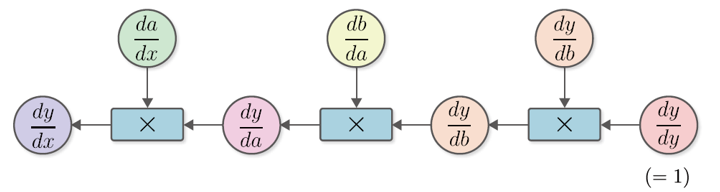
계산 그래프에서 dy/db 는 함수 y = C(b) 의 미분 .. db/da = B'(a), da/dx = A'(x)
이를 이용하여 그래프를 단순화하여 미분값이 전파되는 흐름을 명확히 함

y에 대한 각 변수에 대한 미분 값 : y, b, a, x에 대한 미분값이 오른쪽에서 왼쪽으로 전파 됨 (화살표)
계산 그래프는 역전파를 나타내고 있고 전파되는 데이터는 모두 'y의 미분 값'임
머신러닝은 주로 대량의 매개변수를 입력으로 마지막에 loss function을 거쳐 출력을 내는 형태
손실 함수의 출력은 스칼라 값임 (중요 요소 y)
따라서 역전파를 이용하면 한 번의 전파만으로 모든 매개변수에 대한 미분을 계산할 수 있음을 의미함
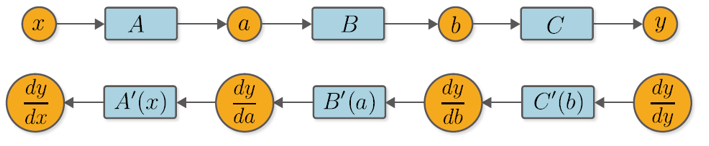
순전파 시의 변수 a는 역전파 시의 미분 dy/da에 대응
순전파 시의 함수 B는 역전파 시의 함수 B'(a)에 대응
변수는 '통상값' 과 '미분값'이 존재하고
함수는 '통상 계산(순전파'과 '미분값을 구하기 위한 계산(역전파)'이 존재
** 역전파 시 순전파 시 이용한 데이터가 필요함
따라서 역전파를 구현하려면 순전파를 먼저 하고 이때 각 함수가 입력 변수의 값을 기억해둔 후 함수의 역전파를 계산
수동 역전파 구현
#역전파에 대응하는 Variable 클래스 구현
#data : 통상값
#grad : 미분값
class Variable:
def __init__(self,data):
self.data = data
self.grad = Noneclass Function:
def __call__(self, input):
x = input.data
y = self.forward(x)
output = Variable(y)
self.input = input # 입력 변수 기억
return output
def forward(self, x):
raise NotImplementedError()
def backward(self, gy):
raise NotImplementedError()메서드의 인수 gy는 ndarray 인스턴스이며, 출력 쪽에서 전해지는 미분값을 전달하는 역할
전달된 미분에 '어떤 함수의 미분'을 곱한 값이 backward의 결과가 된다.
# y = x^2의 미분 dy/dx = 2x
class Square(Function):
def forward(self, x):
return x**2
def backward(self, gy):
x = self.input.data
gx = 2 * x * gy
return gx# y=e^x 의 미분 dy/dx=e^x
class Exp(Function):
def forward(self, x):
y = np.exp(x)
return np.exp(x)
def backward(self, gy):
x = self.input.data
gx = np.exp(x) * gy
return gx

#만들어둔 클래스로 역전파 동작하도록 구현
A = Square()
B = Exp()
C = Square()
x = Variable(np.array(0.5))
a = A(x)
b = B(a)
c = C(b)
y.grad = np.array(1.0)
b.grad = C.backward(y.grad)
a.grad = B.backward(b.grad)
x.grad = A.backward(a.grad)
print(x.grad)
역전파 자동화
일반적인 계산(순전파)를 한 번만 해주면 어떤 계산이라도 상관없이 역전파가 자동으로 이뤄지는 구조 구현
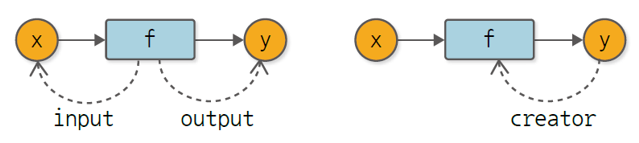
- 변수는 함수에 의해 '만들어진다'
- 함수는 '창조자'
class Variable:
def __init__(self,data):
self.data = data
self.grad = None
self.creator = None
def set_creator(self, func):
self.creator = func#내가 너의 창조자임을 기억시키면서 연결을 동적으로 만듬
class Function:
def __call__(self, input):
x = input.data
y = self.forward(x)
output = Variable(y)
output.set_Creator(self) # 출력 변수에 창조자 설정
self.input = input # 입력 변수 기억
self.output = output # 출력 저장
return output#실행코드
A = Square()
B = Exp()
C = Square()
x = Variable(np.array(0.5))
a = A(x)
b = B(a)
c = C(b)
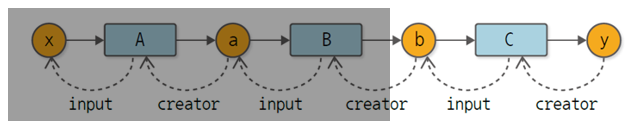
#계산 그래프의 노드들을 거꾸로 거슬러 올라간다.
assert y.creator == C
assert y.creator.input == b
assert y.creator.input.creator == B
assert y.creator.input.creator.input == a
assert y.creator.input.creator.input.creator == A
assert y.creator.input.creator.input.creator.input == xassert 문
조건을 충족하는지 여부를 확인하는 데 사용 가능
assert '주장' 형태로 쓰이며 그 평가 결과가 True가 아니면 예외 발생

역전파 구현
y.grad = np.array(1.0)
C = y.creator # 함수 가져오기
b = C.input # 함수의 입력 가져오기
b.grad = C.backward(y.grad) #함수의 backward 메서드 호출
B = b.creator # 함수 가져오기
a = B.input # 함수의 입력 가져오기
a.grad = B.backward(b.grad) #함수의 backward 메서드 호출
A = a.creator # 함수 가져오기
x = A.input # 함수의 입력 가져오기
x.grad = A.backward(a.grad) #함수의 backward 메서드 호출
print(x.grad)
위의 과정을 자동화
class Variable:
def __init__(self,data):
self.data = data
self.grad = None
self.creator = None
def set_creator(self, func):
self.creator = func
#creator가 None이면 역전파 중단 (함수가 없으므로 인스턴스는 함수 바깥에서 생성됨)
def backward(self):
f = self.creator #함수 가져오기
if f is not None:
x = f.input #함수의 입력 가져오기
x.grad = f.backward(self.grad) #함수의 backward 메서드 호출
x.backward() #하나 앞 변수의 backward 메서드 호출 (재귀)#실행코드
A = Square()
B = Exp()
C = Square()
x = Variable(np.array(0.5))
a = A(x)
b = B(a)
c = C(b)
y.grad = np.array(1.0)
y.backward()
print(x.grad)
* 재귀를 반복문을 이용한 구현으로 변경
복잡한 계산 그래프의 처리 효율은 반복분 방식이 더 좋음
재귀는 함수를 재귀적으로 호출할 때마다 중간 결과를 메모리에 유지하면서 (스택) 처리를 이어가기 때문.
class Variable:
def __init__(self,data):
self.data = data
self.grad = None
self.creator = None
def set_creator(self, func):
self.creator = func
def backward(self):
funcs = [self.creator]
while funcs:
f = funcs.pop() #함수 가져오기
x, y = f.input, f.output #함수 입출력 가져오기
x.grad = f.backward(y.grad) #backward 메서드 호출
if x.creator is not None:
funcs.append(x.creator) #하나 앞의 함수를 리스트에 추가
'코딩 > ML , Deep' 카테고리의 다른 글
| [밑시딥3] 미분 자동 계산 4 - 테스트 (0) | 2023.09.05 |
|---|---|
| [밑시딥3] 미분 자동 계산 3 - 함수를 더 편리하게 (0) | 2023.08.16 |
| [밑시딥3] 미분 자동 계산 1 - 변수, 함수, 수치 미분 (0) | 2023.08.15 |
| 인공 신경망 수식 이해 (0) | 2021.01.18 |


